Regression Analysis
More pages in this category:
# Introduction
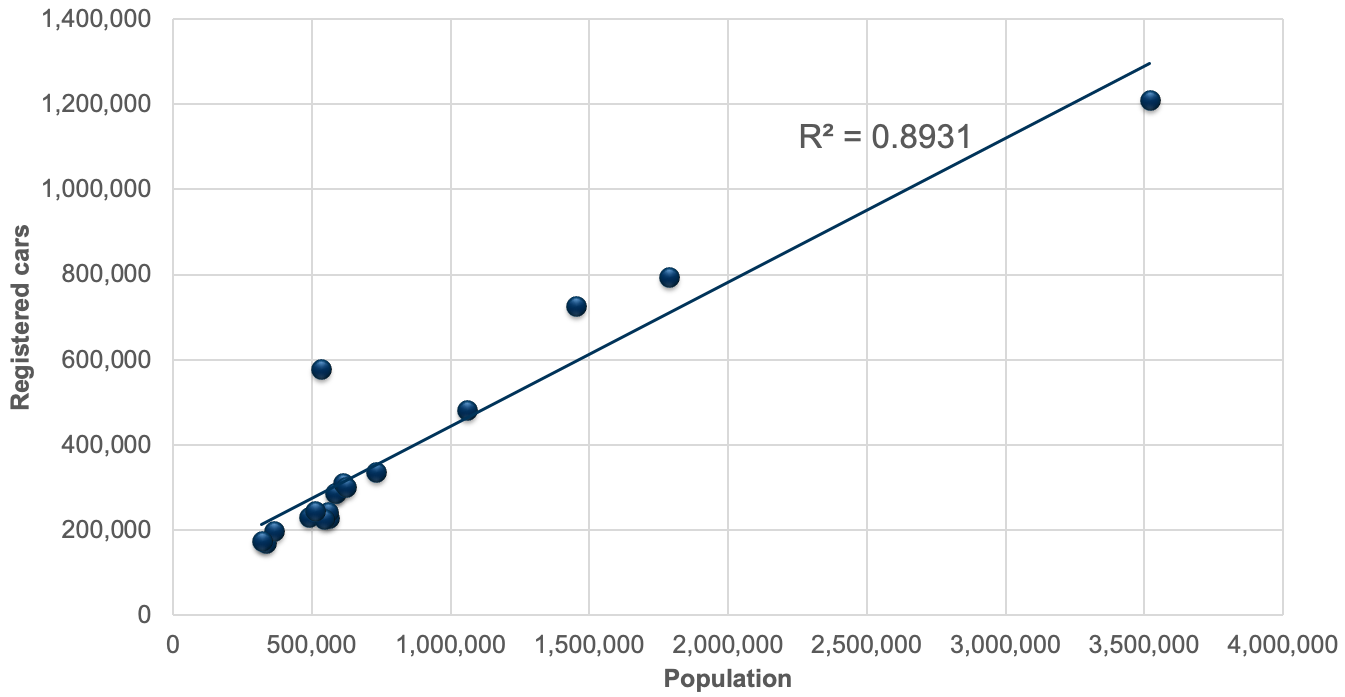
Regression analysis serves to explore the relationship between different variables, such as the number of cars registered in a city and the population of a city. This figure shows that there is -- not surprisingly -- a close relationship between the population in a city and the number of cars registered.
We write can write this relationship as
# Purpose of regression analysis
The goal of regression analysis is to:
- Accurately predict unseen cases.
- Understand which independent variables affect the dependent variable by which degree.
- Assess the quality of the available predictors and inferences.
It should be emphasized that regression analysis only detects correlation, not causation.
# Notation
The function
is a constant a paremeter that defines the impact of population on the number of registered cars is the population in a given city
# Parameter estimation
Using the statistical software R, the coefficients were estimated as:
| Variable | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| (Intercept) | 105752.3 | 1.082e+05 | -1.752 | 0.099 |
| Population | 0.3378216 | 2.287e-01 | 11.562 | 3.52e-09 |
Multiple R-squared: 0.8931, Adjusted R-squared: 0.8864
This estimate can be used in our equation as:
R-squared (or R^2) is an indicator for the model performance. A value closer to 1 suggests that the model is able to represent the observed value very well. A smaller R^2 suggests that the model is missing important variables to explain the dependent variable.
This example shows a linear regression analysis, which is the simplest form of regression analyses. Linear regressions are almost never ''correct'', but a linear model often serves as a good and interpretable approximation to the unknown true function.
# Transformation of variables
It is also possible to apply transformations of independent variables (or even the dependent variable). For example, a polinomial transformation improves the model fit slightly:
| Variable | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| (Intercept) | 104.6245 | 5.99e+04 | 0.00 | 0.099 |
| Population | 0.5518616 | 1.08e-01 | 5.10 | 0.00013 |
| Population^2 | -0.0000000589 | 2.88e-08 | -2.04 | 0.05929 |
Multiple R-squared: 0.916, Adjusted R-squared: 0.905
Using the resulting equation
The most common transformations in regression analysis include:
- Logarithmic transformation:
- Power transformation:
- Polynomial transformation:
# Multiple regression
Multiple regression takes into account more than one variable. The number of registered cars in a city might not only depend on the population but also on other local factors (such as quality of transit, walkability, average income, unemployment rate, etc.). Here, population density was added as a proxy for transit quality and walkability:
| Variable | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| (Intercept) | -34027.57 | 6.79e+04 | -0.50 | 0.624 |
| Population | 0.2843189 | 3.50e-02 | 8.12 | 7.2e-07 |
| PopulationDensity | 70.91963 | 3.11e+01 | 2.28 | 0.038 |
Multiple R-squared: 0.921, Adjusted R-squared: 0.91
Using the resulting equation
Adding more independent variables tends to improve the estimation results, i.e. the R^2 value tends to get larger. However, adding variables should be done with care. Additional variables should only be accepted under the following conditions:
- The estimated parameter is significant. This is indicated by the value in column Pr(>t). If this value is 0.1, it suggests that there is a 10% probability that this parameter was random and does not represent a true relationship in the data. Obviously, this value should be as small as possible. As a rule of thumb, estimates with values greater than 0.1 should be rejected. Exceptions can be made if the value is close to 0.1, and the sign and size of the parameter are as expected and perform well in sensitivity analyses.
- The sign of the estimated parameter is as expected. In the example given above, the sign on the population parameter has to be positive. Otherwise, the model would predict fewer cars for larger cities. For density, one should expect a negative sign, as denser cities tend to have better transit systems and tend to be more walkable. If the sign is the opposite of what should be expected, the variable should be removed.
- The size of the estimated parameter is as expected. Often, this can only be detected through sensitivity analysis. In the example above, one should should take the population and populationDensity of an ''average'' city and adjust the values for population and populationDensity up and down (one at a time). If the parameters are reasonable, the resulting number of registered cars will be plausible.
- The independent variables shall not correlate with each other. If they do, so-called multicollinearity affects the estimation results. Commonly, multicollinearity leads to unexplainable estimated coefficients that result in nonsensical sensitivities.
If two models perform similarly well, but one uses more independent variables, the model with fewer independent variables is commonly preferred.
# Variable interactions#
It is further possible to include interactions between two variables. One could hypothesize, for example, that higher densities only matter in cities with larger population. This effect can be represented by multiplying the two variables with each other.
| Variable | Estimate | Std. Error | t value | Pr(>|t|) |
|---|---|---|---|---|
| (Intercept) | -71567.59 | 1.56e+05 | -0.46 | 0.65 |
| Population | 0.351898 | 2.54e-01 | 1.39 | 0.19 |
| PopulationDensity | 81.14237 | 4.97e+01 | 1.63 | 0.13 |
| Population | -0.00001758771 | 6.54e-05 | -0.27 | 0.79 |
Multiple R-squared: 0.921, Adjusted R-squared: 0.91
In this example, however, all estimated parameters did not reach a significance level of 0.1, and the estimation should be rejected.
← Land Use-Transport Modeling Choice Models - A Self Instructing Course→
